- Défauts de rectitude: Les pièces, après traitement en
laminoirs et diverses manutentions et transports ne sont pas rigoureusement
rectilignes
- Tolérances de laminage: les inerties ne sont pas
constantes
- Défauts de centrage: les efforts normaux de
compression et les appuis ne sont jamais rigoureusement centrés
- Tolérances de montage: les poteaux sur chantiers ne
sont jamais rigoureusement verticaux
- Défauts d’homogénéité: le module d’élasticité E de
l’acier n’est pas vraiment constant, du fait des contraintes résiduelles de
laminage
On représente donc
l’ensemble des imperfections des barres par une courbure initiale, et les
méthodes modernes se différentient essentiellement par la forme qu’elles
entendent donner à celle-ci.
Critère de
résistance:
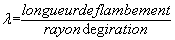 élancement ; l’élancement maximum est de 210
élancement ; l’élancement maximum est de 210
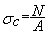 contrainte
de compression
contrainte
de compression
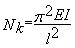 effort
critique d’Euler
effort
critique d’Euler
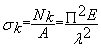 contrainte
critique d’Euler
contrainte
critique d’Euler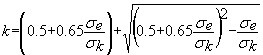 coefficient d’amplification de la contrainte
de compression ; il ne dépend que de l’élancement.
coefficient d’amplification de la contrainte
de compression ; il ne dépend que de l’élancement.
on doit
vérifier que: 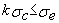
 on a aussi:
on a aussi: 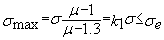 ; utiliser le coefficient k1 est moins contraignant
que le coefficient k (les abaques art 13,411 donnent ce coefficient k)
; utiliser le coefficient k1 est moins contraignant
que le coefficient k (les abaques art 13,411 donnent ce coefficient k) longueurs
de flambements poutres courantes:
avec 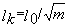
Flambement des pièces treillis: Dans
les pièces treillis, l’effort tranchant, négligeable dans les poutres à âmes
pleines, apporte des contraintes non négligeables. Les règles CM66 art 3,42
donnent la méthode à adopter:
Les tronçons de membrures doivent être vérifiés,
individuellement, par:
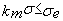
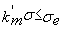
les membrures globalement par:
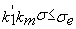 et si
et si 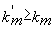 :
:
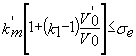
les treillis pour un effort tranchant maximal de:
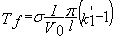
Cas particuliers des membrures et étrésillons de
fermes treillis:
|
Longueur
entre points d’épures lo |
Plan de
la poutre |
Plan ⊥ à la
poutre |
|
Membrures
des poutres à treillis |
0.9lo |
lo |
|
Etrésillons
attachés par un seul rivet |
lo |
lo |
|
Etrésillons
attachés par plusieurs rivets ou soudés |
0.8lo |
lo |
Hypothèses pour l’évaluation des longueurs de
flambement des poteaux: leur évaluation est aisée si l’on
fait les hypothèses simplificatrices suivantes:
- tous les poteaux sont supposés flamber simultanément :
c’est dire qu’aucun poteau, quelque soit son dimensionnement et son niveau de compression, ne contribue à la
stabilité du système
- toute traverse sert simultanément au maintient de deux
poteaux et la rigidité disponible en un nœud est répartie au prorata des
rigidités des poteaux qui y aboutissent
On doit également respecter deux hypothèses sur le
fonctionnement du portique:
- les traverses prises en compte dans la stabilité doivent
être rigidement liées aux poteau par des assemblages d’encastrement sans jeu
- ces même traverses ne doivent être affectées par aucune
perte de rigidité liée à une sollicitation de compression significative
Longueurs de flambement des poteaux: art 5.132
et suivants; on évalue la longueur de flambement des poteaux en évaluant
le coefficient d’encastrement K aux nœuds (entre K=0 articulation parfaite et
K=1 encastrement parfait). Le coefficient K est égal à la somme des rigidités
des poutres et traverses aboutissant au nœud et situés dans le plan de
flambement du poteau à la somme des rigidités de toutes les barres aboutissant
au nœud, poteau compris.
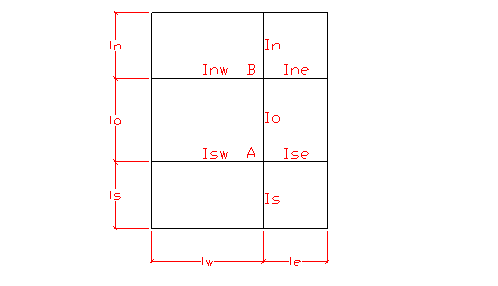
on a
dans le cas ci-dessus: 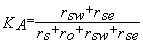 et
et 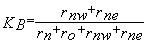
les
rigidités r étant égales à l’inertie de flexion (cm^4) sur la longueur
si un nœud est articulé : K=0
longueur
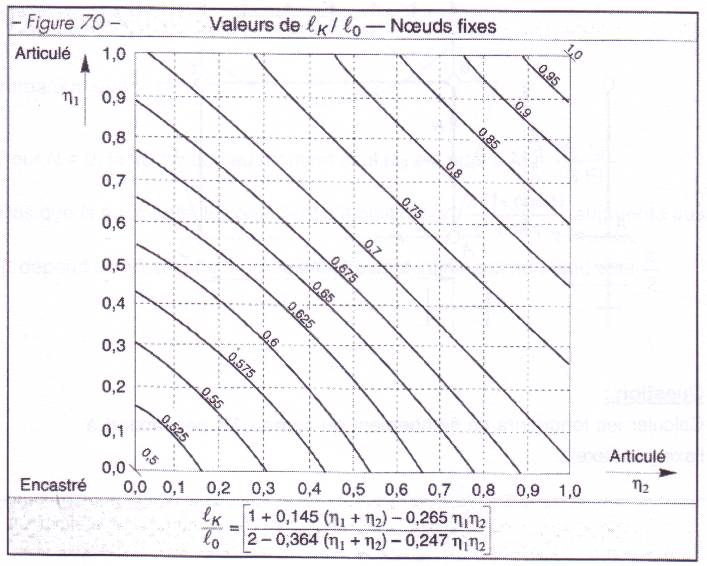
de flambement dans les bâtiments à nœuds fixes: 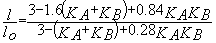
extrémité
B articulée: 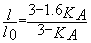
extrémité
B parfaitement encastrée: 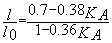
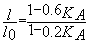
longueurs
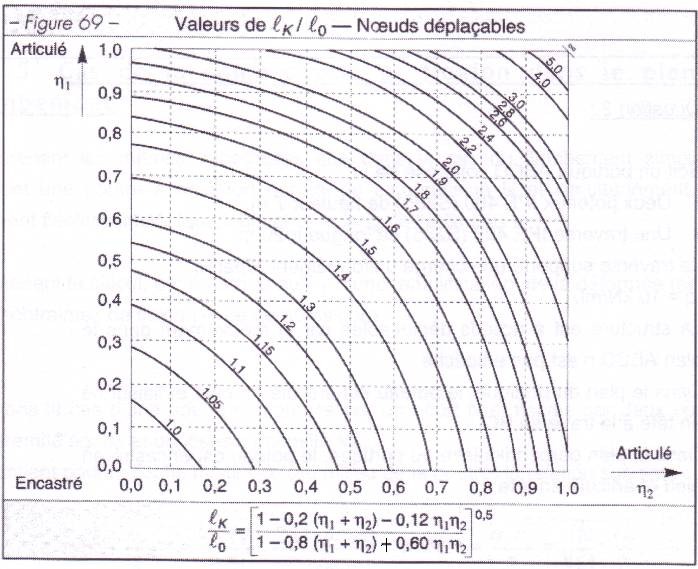
de flambement dans les bâtiments à nœuds libres de se déplacer: 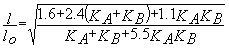
extrémité
B articulée: 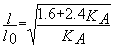
extrémité
B parfaitement encastrée: 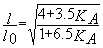
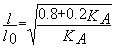
nota: une méthode simplifiée est donnée en annexe 15.134
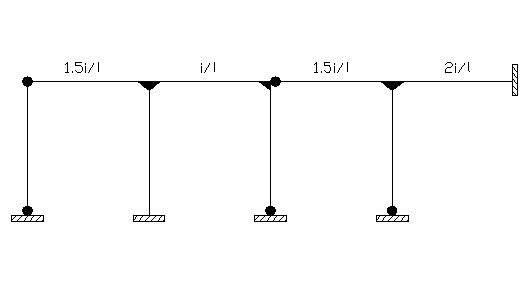
rigidités
des barres dans les bâtiments à nœuds fixes: La rigidité relative I/l
doit être multipliée par:
- 1.5 si
l’extrémité opposée au nœud est articulée (ou plastifiée)
- 2.0 si l’extrémité opposée au nœud est parfaitement encastrée
rigidités
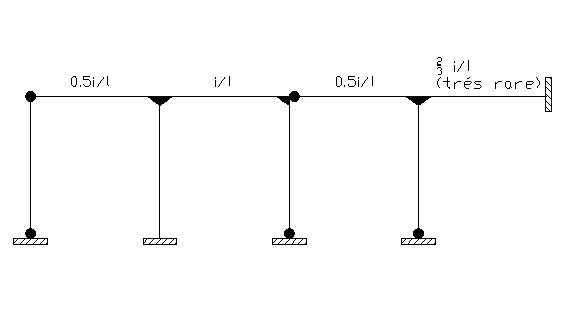
des barres dans les bâtiments à nœuds déplaçables: La rigidité relative
I/l doit être multipliée par
- 0.5 si
l’extrémité opposée au nœud est articulée (ou plastifiée)
- 2/3 si l’extrémité opposée au nœud est parfaitement encastrée
Calcul du flambement selon
l’Eurocode 3:
Prise en compte des
imperfections: il est nécessaires de prendre en compte sous forme
chiffrée les imperfections réelles comme celles de rectitude ou de centrage,
qui font que l’on n’a pas une bifurcation d’équilibre, mais bien une divergence
de plus en plus prononcée qui va conduire la pièce à la ruine dés atteinte d’un
effort normal plus ou moins éloigné de la valeur critique d’Euler, mais
toujours inférieur à celui-ci.
L’eurocode 3 adopte une valeur
initiale sinusoïdale de la déformée
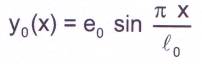

vérification du flambement
simple 5.5.1.1: on doit vérifier que
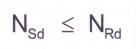
avec
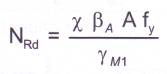

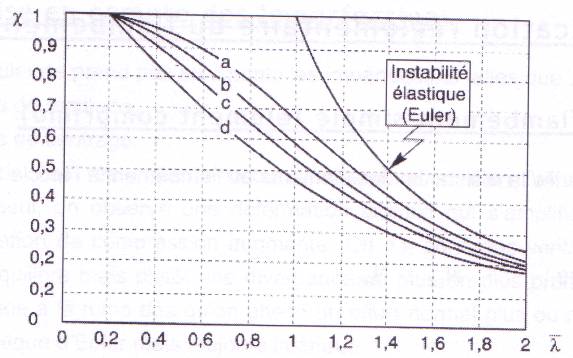
le coefficient c prend en
compte les imperfections de toutes sortes. Pour le déterminer on passe par les
4 courbes de flambement correspondant à une graduation des imperfections
présentées par les barres réelles ; les courbes de flambement dépendent du
type de section, des caractéristiques géométriques ainsi que de l’axe de
flambement :

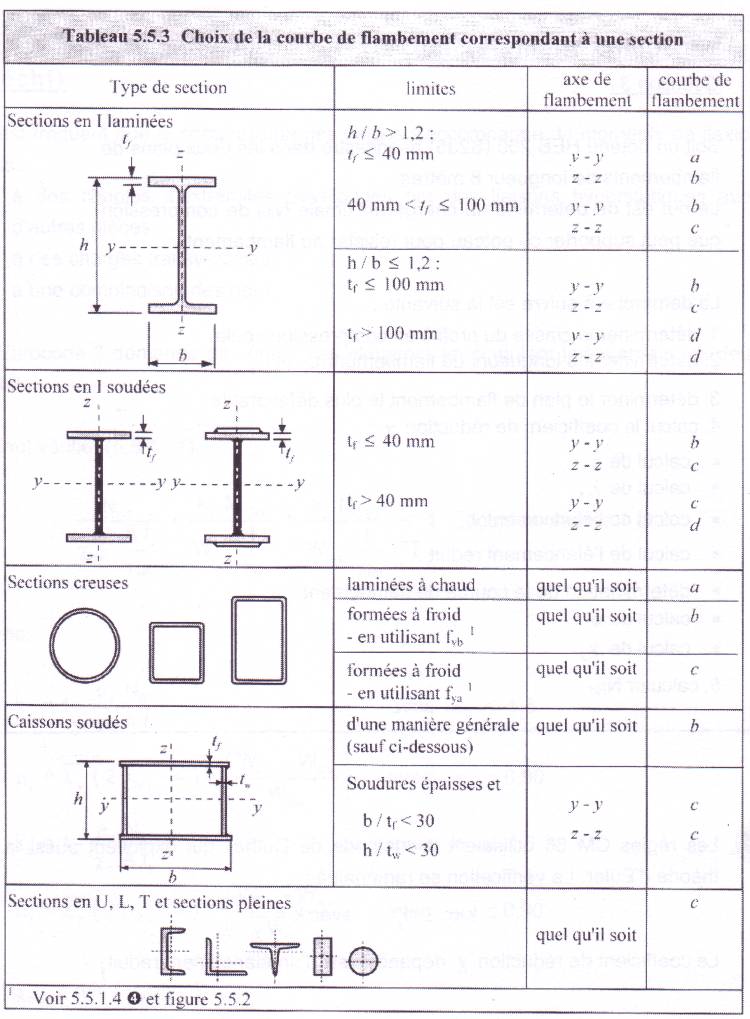
on calcule le coefficient c en
suivant les étapes suivantes 5.5.1.2:

Coefficients théoriques
d’amplifications dus à la flexion:
Avec:
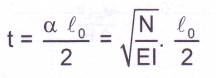

l’Eurocode 3 demande de vérifier
les éléments en cumulant linéairement les effets de la compression et des
moments de flexion ; critère pour les classes 1 et 2 (5.5.4 1):
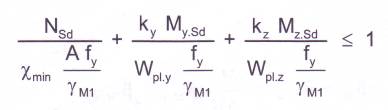
avec:

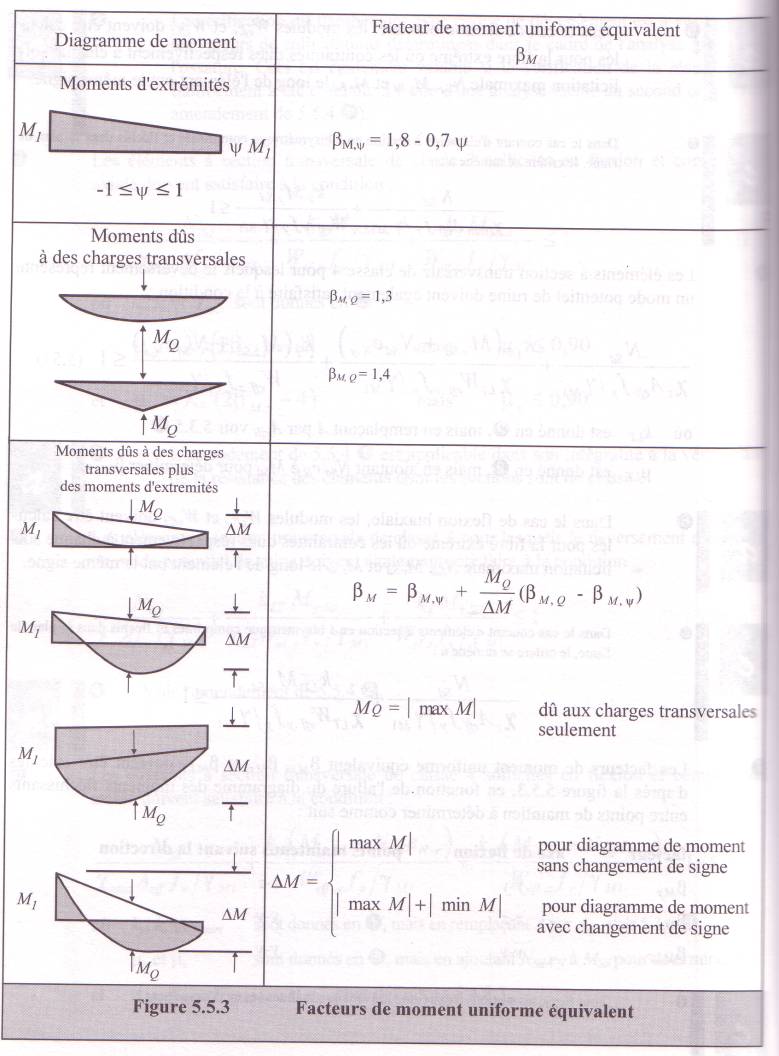

Attention: la
formulation actuelle de l’Eurocode 3 présente des lacunes et des défauts
important qui seront révisés par la norme EN définitive.
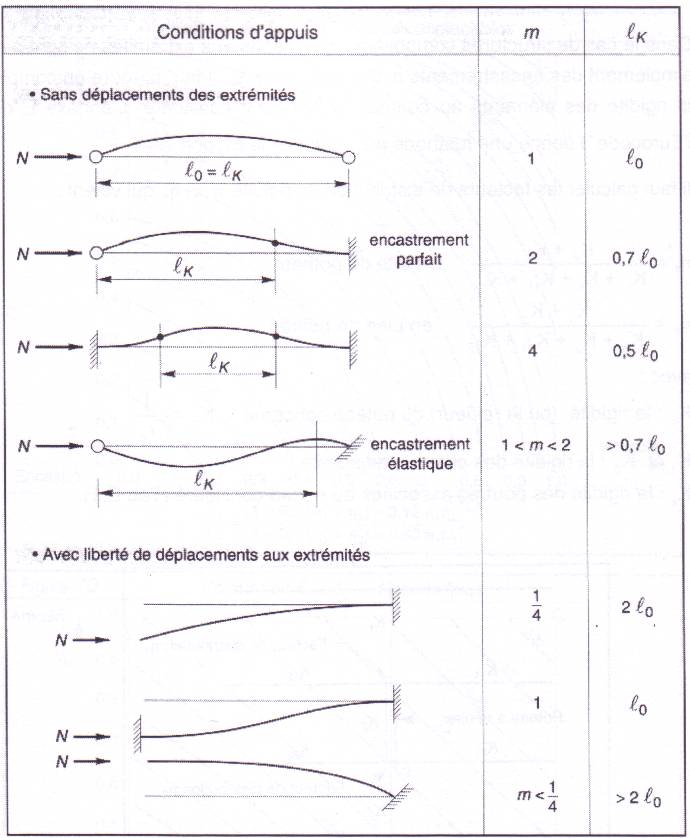
Structures Composées: les
liaisons aux extrémités ne sont ni de simples articulations ni de simples
encastrement. On doit prendre en compte la rigidité des éléments au
contact de l’élément considéré. l’annexe E donne une méthode pour calculer le
rapport lk/l0
calcul des facteurs de
distribution des rigidités (avec I rayon de giration):

pour le
calcul de la rigidité d’une poutre, on doit tenir compte des conditions de
maintien à l’extrémité opposée de celle-ci, voir tableaux E.1 (cas général) et
E.2 (ossatures de bâtiment avec plancher en béton).

on détermine ensuite le rapport
lk/l0 en fonction du type de structures à l’aide des figures E2.1 E2.2 ou des
formules E.2 12: