La cartographie

CARTOGRAPHIE

Ellipsoïde: Pour établir les cartes on doit connaître la forme et les dimensions de la Terre, qui n'est pas sphèrique mais légèrement aplatie aux pôles. On a donc été conduit à adopter un éllipsoïde de référence. Un point quelconque peut donc avoir autant de coordonnées géographiques que de systèmes de références. Historiquement de nombreux ellipsoïdes ont pu être adoptés:

Initialement chaque pays pouvait choisir un éllipsoïde de référence qui suivait au mieux le géoïde sur l'ensemble du pays. La norme mondiale est actuellement le WGS84 (World Geodesic System), utilisée notamment pour le système GPS:

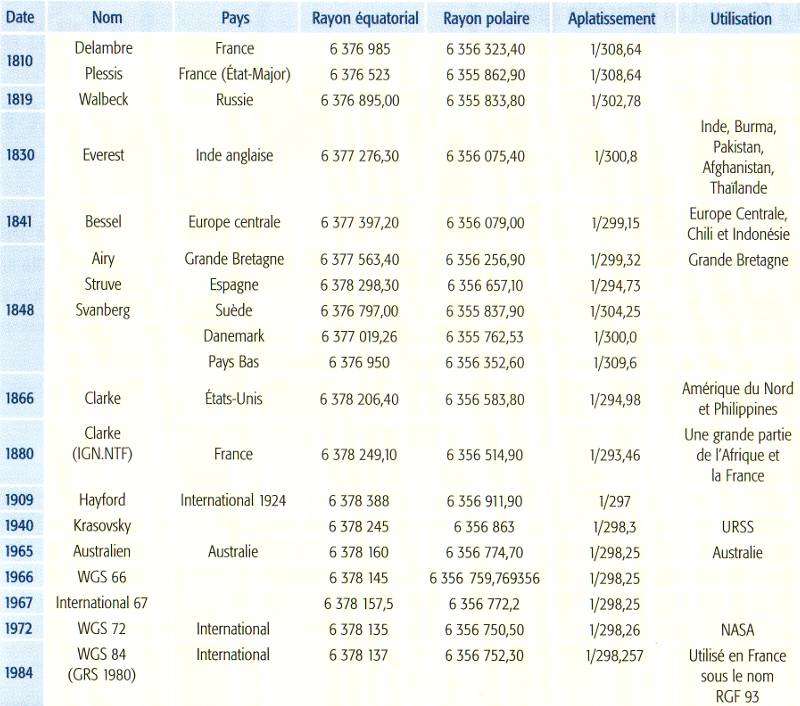
Par définition:

demi grand axe: a=6378137m
aplatissement (a-b)/a: f=1/298,257223563

Par Calcul:

demi petit axe b=6356752m (a(1-f))
première excentricité: e=0,08181919132
deuxième excentricité e'=0,082094438
Circonférence équatoriale: 2xPIxa=40075km
circonférence polaire: 2xPIxb=39940km
surface: 4xPIxR_T²=510065622km²
volume: 4/3xPIxR_T³=1083.10⁹km³

Géoïde: Les allers retours entre les théories et les mesures suscitèrent une question: quelle serait la forme de la terre si elle était recouverte d'eau, c'est à dire la forme de la surface horizontale d'altitude 0 (pour faire abstraction des dénivelées dues aux courants, marées, etc.)? Dés que les mesures ont été suffisamment précises, on se rendit compte que cette surface n'était pas vraiment un éllipsoïde. Un premier indice dans ce sens a été que les triangulations en Europe et en Amérique conduisait à adopter des éllipsoïdes différents. Un second indice a été les mesures du champs de pesanteur qui présentait des singularités.

Le géoïde est donc une équipotentielle du champs de gravité choisie de manière à coller au plus prés de la surface réelle (la gravité dérivant d'un potentiel gravitationel W). Les mesures trés précises des perturbations des trajectoires des satellites artificiels ont montré que le géoïde ne différe d'un éllipsoïde convenablement choisi que par des dépressions et élévations d'au plus 100m. Le géoïde varie dans le temps car:

Il existe des marées terrestres
la tectonique des plaques modifie la répartition des masses
La fonte de glaciers peut relever le niveau de la croûte (e.g. Scandinavie)
etc.

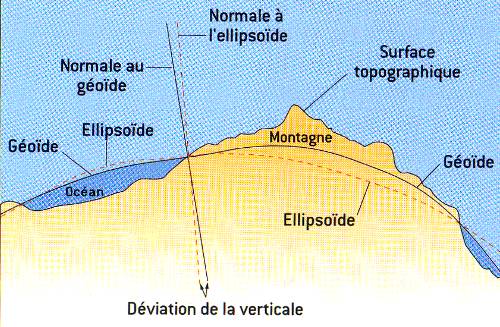
Le repèrage sur le géoïde est un répérage tridimensionnel car aucune symétrie particulière ne permet de choisir des courbes particulières de références.

Systèmes de coordonnées géographiques: les angles sont mesurés en degrés (°, 1/360° tour), minutes (', 1/60° degré) et secondes ('', 1/60 minute). Sur les cartes françaises on emploi parfois les grades (1 angle droit=100 grades).

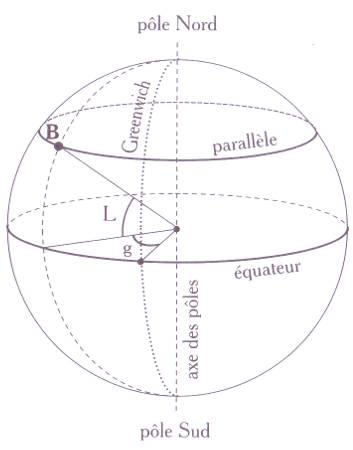
méridiens: demi-cercles qui rejoint les deux pôles; le méridien d’origine est celui de greenwich. Cela donne la mesure de la longitude = angle(méridien-origine, méridien-point), notée g et qui peut être est (E) ou ouest (W) (de 0 à 180°)
parallèles: cercles perpendiculaires à la ligne des pôles; le cercle d’origine est celui de l’équateur. Cela donne la mesure de la latitude = angle(équateur, point-à-déterminer), notée L et qui peut être nord (N) ou sud (S) (de 0 à 90°)
altitudes: En France on se sert de deux références, ayant un caractère permanent et reconnus sans ambiguïté :

référence terrestre: niveau moyen de la mer à Marseille (depuis 1860, maintenant installé dans le marégraphe), niveau moyen qu’on observerait en l’absence de marée dans des conditions atmosphériques standard; il sert à mesurer les altitudes terrestres et les hauteurs des rochers qui dépassent de l’eau même à pleine mer (alias NGF, nivellement général de France).
référence marine: zéro hydrographique, niveau de la plus basse des basses mer astronomique; il sert de référence pour les cartes marines et les annuaires de marée pour définir les profondeurs des mers et les hauteurs d’eau des marées.

Attention: certaines cartes françaises expriment ces coordonnées en grades et prennent généralement pour référence le méridien de Paris, situé à 2°20’14’’ à l’est de Greenwich.

Nord vrai: point de référence correspondant à l’axe imaginaire de rotation de la terre; c’est le haut des cartes, noté 000° ou 360°
Nord magnétique: celui-ci se déplace à la surface du globe; attention, il existe des anomalies magnétiques dans certaines zones, signalées sur les cartes

déplacements sur la sphère terrestre :

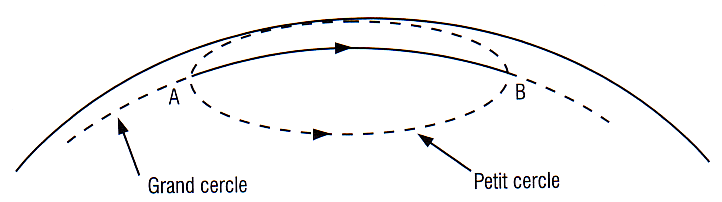
Orthodromie: trajectoire suivant un grand cercle, ligne d’intersection entre la surface terrestre et un plan passant par son centre. il s’agit du plus court chemin sur une sphère. l’équateur est un grand cercle particulier.
Loxodromie: trajectoire suivie lorsqu’on suit toujours la même route vraie; à l’exception de l’équateur les loxodromies sont des petits cercle, lignes d’intersection entre la terre et un plan ne passant pas par son centre.

Distances:

Kilomètres: unité usuelle dans nos contrées
Mille nautique (NM): arc de cercle à la surface de la terre généré par un angle au centre d’une minute d’angle, soit 1.852Km; la vitesse s’exprime alors en mille nautique par heure, appelé nœud (Kt). Il s'agit là d'une unité trés employée par les marins et les aviateurs.
Mile terrestre : 1.609Km; la vitesse associée est le mile terrestre par heure (Mph)

Les cartes: ce sont des représentations planes de la surface terrestre, i.e. projection sphère sur plan, outils pour se repérer et s’orienter. Des graticules représentent les valeurs angulaires des latitudes et longitudes. Cette représentation n’est pas simple car une surface sphérique n’est pas développable et les déformations sont inévitables. On attend deux qualités essentielles des cartes :

conformité: conservation des angles, i.e. un angle sur le plan correspond effectivement à un angle sur la sphère; toutes les cartes aéronautiques ont cette qualité. Dans ce cas l’échelle des longitudes est égale à l’échelle des latitudes
Equidistance: les distances lues sur la carte sont proportionnelles aux distances sur la sphère. Nos cartes ne sont pas rigoureusement équidistantes mais elles conservent à peu prés les distances sur la zone géographique couverte par un feuillet => on peut considérer que l’échelle est la même sur une même carte.

Autres propriétés possibles:

Équivalence: conservation des surfaces. Une surface sur le plan est proportionnelle à la surface sur le géoïde. En général les cartes équivalentes ne sont pas conformes.
Aphylactique: projection ni conforme ni équivalente, mais équidistante

Construction des différentes cartes: on doit établir une correspondance point par point avec la sphère terrestre. Le parallèle d’échelle minimale est le lieu où la surface de projection touche la sphère terrestre.

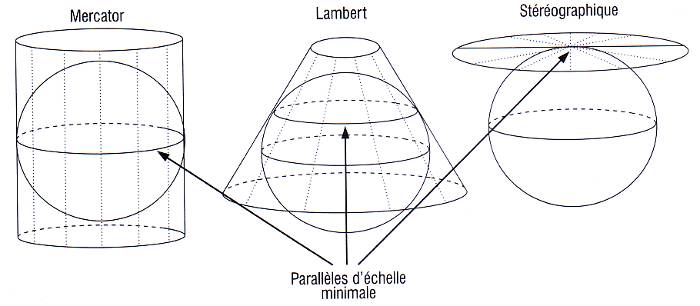
Mercator: adaptée aux latitudes faibles, proches de l’équateur; les méridiens sont des droites verticales équidistantes, les parallèles sont des droites horizontales de plus en plus écartées vers les pôles; ces parallèles donnent l’échelle de latitude, et on peut connaître les distances à condition d’utiliser l’échelle des latitudes correspondante au lieu de la distance à mesurer. Pour cette projection il n’y a pas de déformations pour les surfaces de petites dimensions, et l’échelle est constante autour d’un même point. Les surfaces de grandes dimensions sont quant à elles déformées, les surfaces sur la carte augmentant avec la latitude alors que dans la réalité elles diminuent. Cette projection est trés utilisée pour les cartes marines.

Stéréographique: adaptée aux régions polaires; le centre de projection est le pôle opposé
Lambert: le centre de projection est le centre de la sphère; on peut avoir une ou deux tangences, où l’échelle varie peu; pour la France les géographes prennent souvent 45°N et 49°N. elle est adaptée aux latitudes moyennes:

Méridiens: ils ne sont pas parallèles, mais plus rapprochés vers le nord que vers le sud. Ce sont des droites convergentes.
Parallèles: courbes dont la concavité est orientée vers les pôles.
Orthodromie: on peut considérer qu’il s’agit de droites aux latitudes d’échelles conservées
Loxodromie: courbes dont la concavité est tournée vers le pôle